Al aplicar todos los pasos del
algoritmo Havel-Hakini una sucesión es gráfica si al final todos los elementos
se hacen nulos, pero si existe un elemento que no sea nulo la sucesión ya no es válida.
2.- ¿Cuáles son los pasos del
algoritmo?
*Paso 1: Tenemos una sucesión
decreciente
S, t1, t2,…., tn, d1, d2,…, dn
de la cual eliminamos a S.
*Paso 2: Restamos 1 a los
números anteriores
t1-1,
t2-1,….., tn-1, d1, d2,…, dm
y obtenemos una sucesión más
pequeña, en caso de que alguno de los elementos resulte negativo, la sucesión
ya no es gráfica.
*Paso 3: t1 tomara el lugar de
s.
*Paso 4: Repetiremos los pasos
anteriores hasta que todos los elementos de la sucesión sean nulos.
3.- ¿Explica el ejemplo
planteado en el vídeo?
Tenemos la sucesión decreciente (4, 3, 3, 2,2)
Tomamos el primer término que en este caso será el número 4, lo
eliminamos, a los siguientes cuatro términos les restamos 1.
Nos dará como resultado una
sucesión menor (2, 2, 1,1).
Ahora tomamos a 2 como el
primer término de la sucesión, lo eliminamos, y
a los siguientes dos términos les restamos 1.
Nos dará como resultado una
sucesión menor (1, 0,1), el último paso nos da elementos nulos,
Para finalizar, de la sucesión
anterior re-ordenamos y quitamos el elemento nulo, lo cual nos da (1,1) un grafo
con dos vértices unidos a una arista, esto quiere decir que la sucesión es gráfica.
4.- Resuelve si las siguientes
sucesiones son sucesión gráfica y en su caso elabora la gráfica
correspondiente:
a)
(4, 3, 3, 4, 3, 2, 1) b) (5, 5, 4, 4, 3, 2, 1, 1)
a) Re-ordenando tenemos:
(4, 4, 3, 3, 3, 2,1)
La sucesión no es gráfica porque
al final del algoritmo no todos los elementos se hacen nulos.
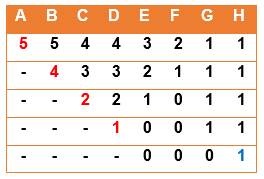
b) (5, 5, 4, 4, 3, 2, 1,1)
La sucesión no es gráfica porque
al final del algoritmo no todos los elementos se hacen nulos.