lunes, 6 de junio de 2016
Tarea 4: E-book unidad 5 y 6
https://issuu.com/gabsodair/docs/ebookdocx
miércoles, 11 de mayo de 2016
Biografías
Philip Hall
Philip Hall
[Fotografía] Recuperada 11 de mayo 2016
https://es.wikipedia.org/wiki/Philip_Hall#/media/File:Philip_Hall.jpg
Nació el 11 de
abril de 1904, Hampstead, Reino Unido en 1911.
Fue un matemático inglés. La mayor parte de su
trabajo se centró en teoría de grupos, notablemente en grupos finitos
En mayo de 1915 a los once años ganó una beca para el Hospital
West Horsham de Cristo. Aunque estos fueron los años de la Primera Guerra Mundial, Hall
era demasiado joven para ser afectado por la guerra, aparte de servir en el
Cuerpo de Entrenamiento de Oficiales.
Fue en el hospital de Cristo que llegó a amar las matemáticas. Tuvo la suerte de tener maestros que eran matemáticos
consumados, ellos decían que Hall no sólo eran las
matemáticas, gano la medalla de oro en su último año, pero también en Inglés,
gana una medalla por el mejor ensayo.
El interés de Hall en la teoría de grupos procedía
de Burnside libro que se le animó a leer por Arthur Berry, el Tutor
Asistente de Matemáticas en el Colegio del Rey. En octubre
de 1926 presentó un ensayo sobre “Los Isomorfismos de grupos abelianos”. Fue elegido miembro de la
Royal Society en 1951 y
concedió su Medalla Sylvester en 1961. Fue Presidente de la Sociedad Matemática de Londres en 1955 hasta 1957, y concedió su Premio
Berwick en 1958
y Medalla De Morgan en 1965. Muere el 30
de diciembre 1982,
en Cambridge, Inglaterra.
Referencias:
https://es.wikipedia.org/wiki/Philip_Hall
https://translate.google.com.mx/translate?hl=es-419&sl=en&u=http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Hall.html&prev=search
Vojtěch Jarník [Fotografía] Recuperada 11 de mayo 2016
Vojtěch Jarník (22 de diciembre de 1897 - 22 de septiembre de 1970)
fue un matemático checo. Su principal área de trabajo fue en la
teoría de los números y el análisis matemático, demostró una serie de
resultados en problemas de puntos de retículos. También descubrió el algoritmo sobre la teoría de
grafos conocido como el algoritmo de Prim, el
cual después desarrollaría Robert C. Prim en los laboratorios
Bell .
Referencias:
Vojtěch Jarník [Fotografía] Recuperada 11 de mayo 2016
http://america.pink/jarnik_2190048.html
Vojtěch Jarník (22 de diciembre de 1897 - 22 de septiembre de 1970)
fue un matemático checo. Su principal área de trabajo fue en la
teoría de los números y el análisis matemático, demostró una serie de
resultados en problemas de puntos de retículos. También descubrió el algoritmo sobre la teoría de
grafos conocido como el algoritmo de Prim, el
cual después desarrollaría Robert C. Prim en los laboratorios
Bell .
Como graduado Vojtěch Jarník se unió
en 1915 para estudiar matemáticas y física en
la Universidad Charles en Praga.
En 1929 fue nombrado profesor Adalberto
Jarnik asociado de matemáticas en la Universidad Charles y seis años más tarde,
un profesor de tiempo completo. En la universidad trabajó
hasta 1967 , cuando se retiró. Después de la creación de la
Academia de Ciencias de Checoslovaquia fue
en 1952 nombrado académico y se convirtió en el primer
presidente de la sección de matemáticas y física.
Vojtěch Jarník interesado en la historia de las
matemáticas, con atención especial para estudiar las obras de Bernard
Bolzano . El foco principal de su trabajo ha sido el área de la
teoría de números y el análisis matemático
Publico cuatro volúmenes de libros de texto serie
de análisis matemático, que todavía se utiliza hoy en día:
* Introducción al cálculo integral parte
1 ( 1938 ) se basa en Kösslerův Introducción del
diferencial.
*Introducción
al cálculo diferencial parte 2 ( 1946 ), y más tarde
( 1948 ), complementado por una extensa introducción a números
enteros
Referencias:
https://translate.google.com.mx/translate?hl=es-419&sl=cs&u=https://cs.wikipedia.org/wiki/Vojt%25C4%259Bch_Jarn%25C3%25ADk&prev=search
https://es.wikipedia.org/wiki/Vojt%C4%9Bch_Jarn%C3%ADk
Joseph Kruskal
Joseph B. Kruskal [Fotografía] Recuperada 11 de mayo 2016
Joseph B. Kruskal (29 de enero de 1928 – Maplewood, Nueva Jersey, 19 de septiembre de 2010) fue un matemático y estadístico estadounidense.
Referencias:
Joseph Kruskal
Joseph B. Kruskal [Fotografía] Recuperada 11 de mayo 2016
http://www.nytimes.com/2007/01/13/obituaries/13kruskal.html?_r=0
Joseph B. Kruskal (29 de enero de 1928 – Maplewood, Nueva Jersey, 19 de septiembre de 2010) fue un matemático y estadístico estadounidense.
Investigador
del Math Center (Bell-Labs),
en 1956 descubrió un algoritmo para la
resolución del problema del árbol de coste total mínimo (mínimum spanning tree –
MST). El cual es un problema típico de optimización combinatoria, que fue considerado originalmente por Otakar Boruvka (1926)
mientras estudiaba la necesidad de electrificación rural en el sur de Moravia en Checoslovaquia.
El
objetivo del algoritmo de Kruskal es
construir un árbol (subgrafo sin ciclos) formado por arcos sucesivamente
seleccionados de mínimo peso a partir de un grafo con
pesos en los arcos. Un árbol (spanning tree) de un grafo es
un subgrafo que contiene todos sus vértices o nodos.
Un grafo puede tener múltiples árboles. Por ejemplo, un grafo completo de cuatro nodos (todos
relacionados con todos) tendría 16 árboles.
La
aplicación típica de este problema es el diseño de redes telefónicas. Una
empresa con diferentes oficinas, trata de trazar líneas de teléfono para
conectarlas unas con otras. La compañía telefónica le ofrece esta
interconexión, pero ofrece tarifas diferentes o costes por conectar cada par de
oficinas. Cómo conectar entonces las oficinas al mínimo coste total.
La
formulación del MST también ha sido aplicada para hallar soluciones en diversas
áreas (diseño de redes de transporte, diseño de redes de telecomunicaciones -
TV por cable, sistemas distribuidos, interpretación de datos climatológicos,
visión artificial - análisis de imágenes - extracción de rasgos de parentesco,
análisis de clusters y búsqueda de súper-estructuras, plegamiento de proteínas,
reconocimiento de células cancerosas, y otros).
Joseph era hermano del matemático y estadístico William Kruskal (autor
de la Prueba de Kruskal-Wallis), y del matemático y físico Martin Kruskal (autor
de las coordenadas de Kruskal-Szekeres).
Referencias:
https://es.wikipedia.org/wiki/Joseph_Kruskal
viernes, 6 de mayo de 2016
lunes, 2 de mayo de 2016
domingo, 1 de mayo de 2016
domingo, 3 de abril de 2016
Unidad 2: Participación 2
|
Unidad 2 Representación Algebraica
|
Participación 2
|
Matriz de
adyacencia
Sube el ejercicio 2
a tu blog
|
Unidad 2: Participación 7
Unidad 1: Participación 3
Biografías Havel - Hakimi
1.- Václav J. Havel
Václav J. Havel [Fotografía] Recuperada 3 de abril 2016
http://www.quotecollection.com/image-view.php?img=vaclav-havel-4.jpg
Matemático de origen checo, que se dedicó al estudio de la teoría de
grafos, su trabajo más importante en 1955 fue la solución al problema para la
secuencia de enteros gráfica, tiempo después fue resuelta
independientemente por Hakimi.
Sus trabajos más importantes:
*Havel publicó alrededor de 90 artículos matemáticos en diferentes
revistas entre los años 1955 y 1994.
*El problema de la secuencia de enteros gráfica: El cual consiste en
determinar si una secuencia de enteros no negativos cualquiera es o no gráfica.

Referencias:
2.- S. L Hakimi
S. L Hakimi [Fotografía] Recuperada 3 de abril 2016
https://calisphere.org/item/ark:/13030/kt500040nj/
Seifollah Louis Hakimi matemático nacido en Irán, fue maestro en la
universidad de Northwestern, especializándose en el departamento de ingeniería
eléctrica, desde 1973 a 1978.
Cuenta con más de 100 descendentes académicos, la mayoría a través de su
alumno Narsingh Deo.
Sus trabajos más importantes:
*Caracterizo las secuencias de grado para grafos no dirigidos, para la
formular el problema al árbol de Steiner en las redes, también realizo un
trabajo sobre localización de servicios y problemas en las redes.
miércoles, 23 de marzo de 2016
viernes, 4 de marzo de 2016
Tarea 1: Presentacion de los conceptos unidad 1
Integrantes del equipo:
Salazar Silva Gabriela
Guerrero Ferrusca Nayely
Andrea
martes, 9 de febrero de 2016
Unidad 1: Introducción a la Teoría de Gráficas, Tarea 1
Al aplicar todos los pasos del
algoritmo Havel-Hakini una sucesión es gráfica si al final todos los elementos
se hacen nulos, pero si existe un elemento que no sea nulo la sucesión ya no es válida.
2.- ¿Cuáles son los pasos del
algoritmo?
*Paso 1: Tenemos una sucesión
decreciente
S, t1, t2,…., tn, d1, d2,…, dn
de la cual eliminamos a S.
*Paso 2: Restamos 1 a los
números anteriores
t1-1,
t2-1,….., tn-1, d1, d2,…, dm
y obtenemos una sucesión más
pequeña, en caso de que alguno de los elementos resulte negativo, la sucesión
ya no es gráfica.
*Paso 3: t1 tomara el lugar de
s.
*Paso 4: Repetiremos los pasos
anteriores hasta que todos los elementos de la sucesión sean nulos.
3.- ¿Explica el ejemplo
planteado en el vídeo?
Tenemos la sucesión decreciente (4, 3, 3, 2,2)
Tomamos el primer término que en este caso será el número 4, lo
eliminamos, a los siguientes cuatro términos les restamos 1.
Nos dará como resultado una
sucesión menor (2, 2, 1,1).
Ahora tomamos a 2 como el
primer término de la sucesión, lo eliminamos, y
a los siguientes dos términos les restamos 1.
Nos dará como resultado una
sucesión menor (1, 0,1), el último paso nos da elementos nulos,
Para finalizar, de la sucesión
anterior re-ordenamos y quitamos el elemento nulo, lo cual nos da (1,1) un grafo
con dos vértices unidos a una arista, esto quiere decir que la sucesión es gráfica.
4.- Resuelve si las siguientes
sucesiones son sucesión gráfica y en su caso elabora la gráfica
correspondiente:
a)
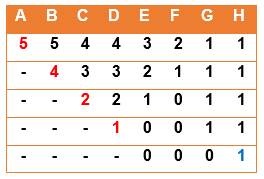
(4, 3, 3, 4, 3, 2, 1) b) (5, 5, 4, 4, 3, 2, 1, 1)
a) Re-ordenando tenemos:
(4, 4, 3, 3, 3, 2,1)
La sucesión no es gráfica porque
al final del algoritmo no todos los elementos se hacen nulos.
b) (5, 5, 4, 4, 3, 2, 1,1)
La sucesión no es gráfica porque
al final del algoritmo no todos los elementos se hacen nulos.
Suscribirse a:
Comentarios (Atom)